Som jeg skrev i artikkelen om valutasikring av balanserisiko kan et selskap med betingelser (covenants) i sine låneavtaler være nødt til å sikre risiko på balansen, selv om det ikke nødvendigvis er optimalt.

Men hvordan kan selskapet vite hvilket nøkkeltall det er viktigst å sikre?   Ofte vil selskapet ha mer enn en covenant, og sikring av den ene vil kunne ha negativ effekt på den andre. For å få svar på det er det nødvendig å regne på effekten av sikring, og den beste måten å gjøre det på er ved hjelp av en simuleringsmodell. En slik modell vil kunne gi svaret i form av f.eks. sannsynligheten for å bryte en betingelse i en låneavtale.

Hvilken sikringsstrategi som velges vil jo nettopp være avhengig av kunnskap om dette – hvor sannsynlig er det at selskapet vil komme i brudd? Som jeg beskrev i den forrige artikkelen:

Valg av sikringsstrategi er avhengig av hvilket nøkkeltall som er mest risikoutsatt. Det er iboende motsetninger mellom ulike sikringsstrategier og det er derfor nødvendig med en grundig gjennomgang før sikring implementeres.

Og i tillegg:

Dersom selskapet sikrer gearing, vil selve egenkapitalens størrelse være mer utsatt for svingninger [..]. Dessuten er det ofte slik at det å trekke gjeld i funksjonell valuta innebære en økning av selskapets økonomiske risiko [..]. Dersom selskapet ikke må sikre gearing, bør selskapet derfor heller sikre egenkapitalen.
En sikring av egenkapital ligger nærmest opp mot sikring av markedsverdi. Sikring av gearing er ikke optimalt, og bør bare iverksettes dersom det er nødvendig.

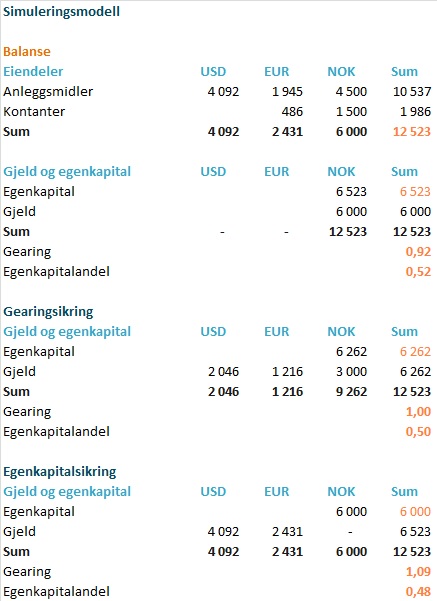
For å analysere effekten of different strategies og forsøke å svare på spørsmålene over, har jeg bygget inn simulering av valutakursene med utgangspunkt i samme eksempel som i forrige artikkel:

Resultatet av ulike strategier ved en 10% endring av valutakurser opp og ned viste jeg i forrige artikkel. Men den modellen kan ikke gi svar på hvor sannsynlig brudd på covenants er. Hvor store valutakursendringer tåler selskapet?

For å se på dette har jeg tatt utgangspunkt i følgende modellering av valutakursene:

• Sluttkursene ved hvert kvartalsslutt fra 31/12/2002 til og med 30/06/2013. Grunnen til at jeg har valgt akkurat de datoene er selvsagt at det er på de datoene balansen måles. Det spiller liten rolle om valutakursen er helt grei den 1.mars om den ikke er det den 31.mars. For da avsluttes regnskapet for Q1 og da måles balansen.

• Disse sluttkursene har jeg analysert med Excel @Risk, som kan lage en sannsynlighetsfordeling basert på historiske tallrekker. Det er selvsagt mange måter å sette sannsynlighet for en valutakurs på, det skal jeg komme tilbake til ved en senere anledning, men denne metoden har mye for seg – tross alt er utgangspunktet en virkelig utvikling.

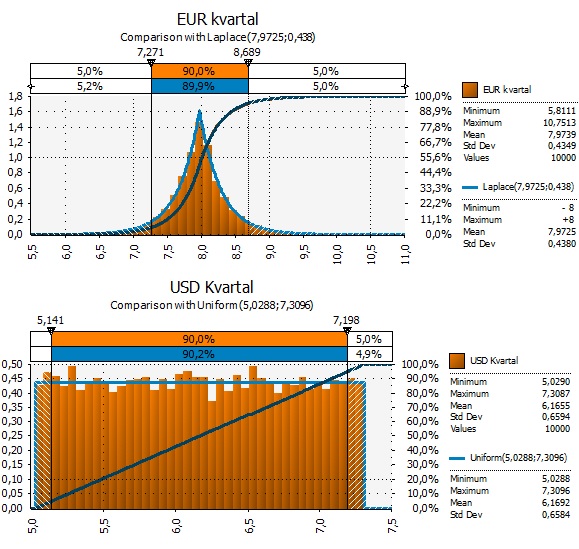
De best egnede kurvene den fant var en LapLace-kurve ((RiskLaplace (μ,σ) specifies a laplace distribution with the entered μ location and σ scale parameters. The laplace distribution is sometimes called a “double exponential distribution” because it resembles two exponential distributions placed back to back, positioned with the entered location parameter.)) for EUR og en Uniform-kurve ((RiskUniform(minimum,maximum) specifies a uniform probability distribution with the entered minimum and maximum values. Every value across the range of the uniform distribution has an equal likelihood of occurrence)) for USD.

Det er alltid en god ide å spørre seg selv om det ligger en god historie bak et slikt forslag.  Virker det logisk? Det vi er ute etter er tross alt å finne et så godt estimat for fremtidige valutakurser som mulig. Om vi ikke finner logikk, bør vi går tilbake og analysere mer.  Men det er god logikk å se i disse kurvene, synes jeg:

• EUR er såkalt Mean reverting, hvilket vil si at den som etter en periode kommer tilbake til et gjennomsnittsnivå på rundt 8 kr +/-.  Dermed blir kurven spiss og har lange haler.  Det er mest sannsynlig at vi må betale 8 NOK for 1 EUR, men den kan bevege seg mye både opp og ned.

• USD er en mer uforutsigbar valuta og det virker ikke dumt å si at de fleste USD-nivåer har like stor sannsynlighet.

I tillegg til sannsynlighetskurvene for USD og EUR trengs det et estimat for samvariasjonen mellom dem. Der brukte jeg de samme historiske dataene til å beregne historisk korrelasjon. På sluttkursene har den vært 0,39. Det vil si at det ikke er slik at om den ene går opp, går den andre ned. Årsaken til det er selvsagt at det er den norske kronen som beveger seg. NOK går mot både USD og EUR. Heller ikke en dum forutsetning.  Slik har det vært de siste 10 årene.

Da har vi den informasjonen som trengs for å kunne simulere hvor utsatt vår (enkle) balanse er for valutakursendringer. Og basert på simuleringen er svaret: en hel del.

Jeg har sett på følgende covenants:

• Gearing < 1,5
• Egenkapital > 3 000

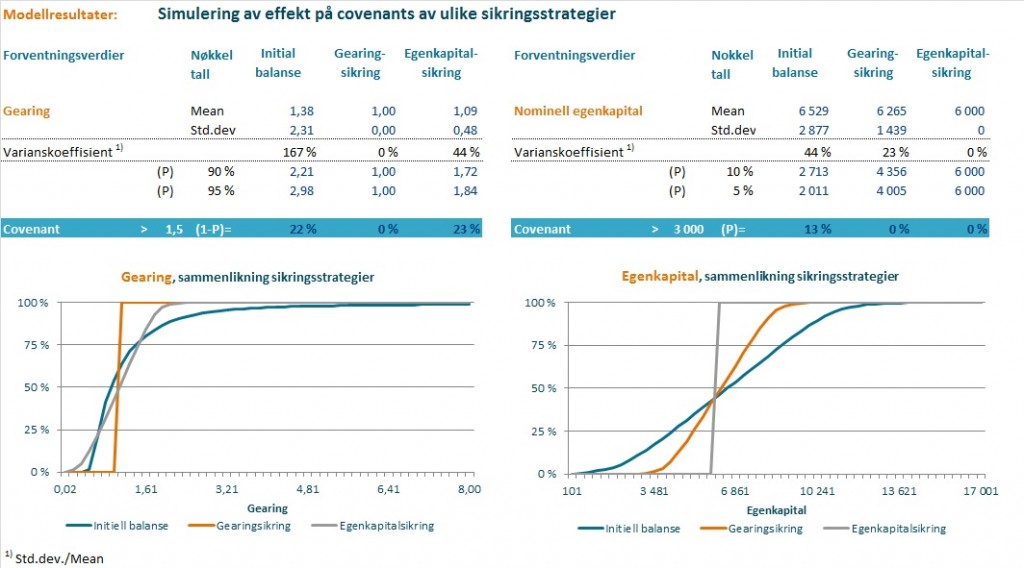
Slik ble resultatet av simuleringen (klikk på bildet for å forstørre):

Som tabellene/grafene viser er gearing (gjeld/egenkapital) det mest sårbare nøkkeltallet. Både i den opprinnelige mixen, med bare gjeld i NOK og dersom selskapet egenkapitalsikrer er det ganske stor sannsynlighet for at et brudd på gearing-covenant.

Det er en sannsynlighet på 22% i det første tilfellet og en sannsynlighet på 23% i det andre. Det er ganske høy sannsynlighet når vi vet at NOK kan bevege seg ganske mye, ganske fort.

Egenkapitalen er mer robust. Det er en 13% sannsynlighet for brudd med all gjeld i NOK, men 0% dersom selskapet velger en av de to sikringsstrategiene. Det skyldes selvsagt at lån i valuta, uansett om det ikke er like mye som eiendelene vil redusere risikoen.

Dermed er det i dette eksempelet enkelt å gi råd til selskapet. Det bør sikre gearing, ved å trekke gjeld i valuta i samme miks som eiendelene. Virkeligheten er selvsagt mer kompleks enn dette eksempelet, men mekanismen vil være det samme. Og behovet for å vite hvor sannsynlig det er at selskapet kan komme i brudd er enda større i en mer kompleks virkelighet.

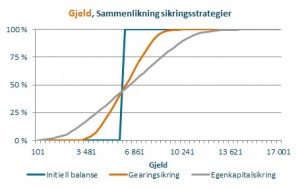En ting som kompliserer bildet er påvirkningen på selskapets gjeld.  Den kan variere kraftig, avhengig av strategi.

Dersom selskapet må refinansiere noe av gjelden, og samtidig får en for gjelden negativ utvikling (svakere hjemmevaluta) vil refinansieringsbehovet kunne være vesentlig større enn selskapet ville hatt dersom gjelden hadde vært beholdt i hjemmevalutaen.  Dette er også svar som en simulering kan gi.

Svaret på spørsmålene «Hvor sannsynlig er brudd på en covenant og hva er konsekvensene av ulike strategivalg på nøkkeltall, gjeld og egenkapital?» er det egentlig bare en god simuleringsmodell som kan gi.