Et estimat på variabilitet er den viktigste input’en i en risikomodell.  Risiko oppstår fordi de faktiske variabelverdiene avviker fra forventet verdi.  Derfor er det første spørsmålet man må stille seg for å kunne estimere risiko: Hvor mye kan variablene forventes å avvike fra forventet verdi?

Om du ikke forventer noe avvik er variabelen å anse som deterministisk – eller som en kjent størrelse.  Svært få variable er selvsagt det, men jeg er tilhenger av å modellere volatilitet på få, men viktige variable . Dermed kan noen variable, de som ikke har så stor betydning, anses som kjente selv om de ikke er det.

Volatilitet kan estimeres på flere måter, blant annet:

• Beregnes basert på historiske tidsserier
• Implisitt volatilitet, som vil si at det finnes markedspriser for volatilitet (som for eksempel for kraftpriser eller valutakurser)
• Estimert volatilitet basert på egne forutsetninger om fremtidig volatilitet, dersom markedspriser ikke finnes

Den inputen vi får fra disse metodene brukes til å sette sannsynlighetsfordelinger.  Det kan gjøres på ulike måter.

• Standardavvik
  eller gjennomsnittlig avvik fra gjennomsnittsverdi ((For å være presis så er std.dev. kvadratroten av variansen)).  Dersom en normalfordeling kan brukes, beskriver standardavvik risikoen.  Men verden er sjelden normal, og dermed er normalfordelingen ikke så ofte egnet.

• Høy, lav og forventet verdi
  Å sette forventet verdi, en høy og lav verdi definerer en sannsynlighetskurve.   Jeg er tilhenger av å gjøre forenklinger, så jeg bruker veldig få kurvetyper.  Det finnes en lang rekke mulige fordelinger, men egentlig trenger du bare noe få som i de fleste tilfeller gir en mer enn god nok modellering.

• Fit til historiske data
  Her bruker du historiske data til å estimere en kurve.  Dette er en funksjon i f.eks. Excel @Risk.  Den har en lang rekke mulige distribusjoner og estimerer hvilken som vil kunne passe best basert på data.  Problemet med mange av disse er at de er til dels komplekse å forstå og ikke minst vanskelige å vedlikeholde data til ((De krever spesielle parametere for å beregne kurven; stort sett en lang rekke mer eller mindre begripelige greske bokstaver)).  Jeg unngår de mer spesielle variantene med mindre de er de eneste som vil beskrive en variabel på en god måte.

Jeg bruker ofte triangulære fordelinger i min modellering, eller en kurve som heter Pert og ligner på den triangulære fordelingen ((The PERT distribution (meaning Program Evaluation and Review Technique) is rather like a Triangular distribution, in that it has the same set of three parameters. Technically it is a special case of a scaled Beta (or BetaGeneral) distribution. In this sense it can be used as a pragmatic and readily understandable distribution.  It can generally be considered as superior to the Triangular distribution when the parameters result in a skewed distribution, as the smooth shape of the curve places less emphasis in the direction of skew.)).  Den kan enten settes med minimum og maksimum-verdier eller ved på bestemte sannsynlighetsnivåer.   Med mindre halene er veldig skjeve fungerer den riktig bra.  Det leder oss til det neste spørsmålet det er nødvendig å stille:

Hvordan ser kurven ut?

Dette er et særdeles viktig tema– nemlig nødvendigheten av å ha et forhold til fasongen på sannsynlighetskurven.  Som sagt er verden sjelden normal, og dermed har de fleste fordelinger en skjevhet den ene eller den andre veien.  Det er nødvendig å ha forstå og bruke et begrep fra statistikken. Det sier noe om hvor skjev kurven er og heter skewness.

Heldigvis er ikke dette tall vi må håndregne, det finnes det enkle og billige statistikkprogrammer som kan gjøre for oss.  Jeg bruker StatTools fra Palisade, men du kan til og med regne det ut på data ved å bruke en statistikkfunksjon i Excel (SKEW).  Det viktige er å forstå hva det betyr for risiko.

Dersom en kurve har like haler til høyre og venstre er tallet Skewness=0.  Er Skewness <0 har fordelingen lengre eller fetere hale til venstre, er Skewness > 0 er den lengre eller fetere til høyre.  Altså:

• =0 Normal
• <0 Skjev venstre
• >0 Skjev høyre

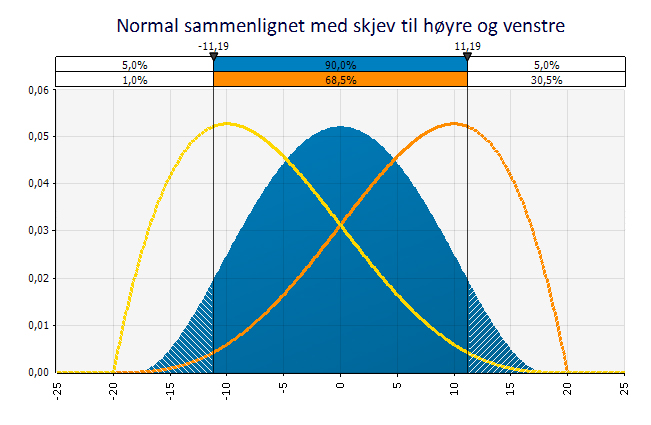
Grafen under viser en normalfordeling med kurver med hale til høyre og venstre lagt oppå.

Kurvene har samme ytterpunkter (-20, +20) men ulik forventningsverdi (0, -10, +10).  Kurven med hale til venstre har en skjevhets på -0,5 og den med hale til høyre har en skjevhet på +0,5.

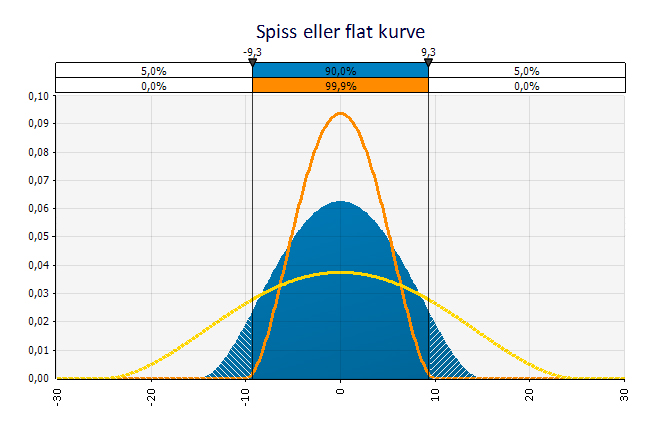
I tillegg bør du da et blikk på kurven og se hvor spiss eller flat den er.  Dersom kurven er spiss vil det si at observasjonene faller innenfor et smalere utfallsrom enn dersom den er flat.  Det er en god tommelfingelregel at jo flatere kurve, jo mer risiko.

Modellering av spotprisen på Nordpool

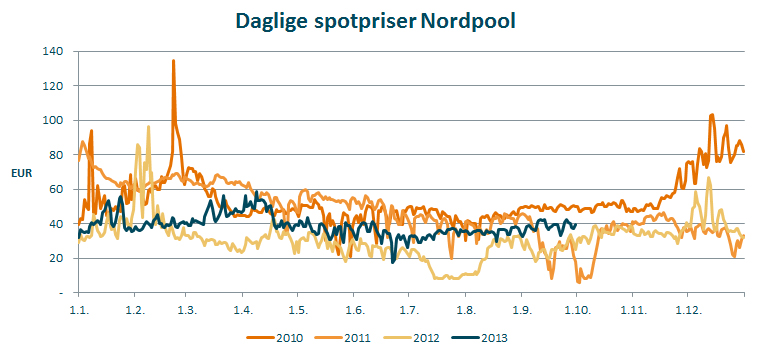
Jeg har hentet spotpriser for kraft fra Nordpool spot for å vise hvordan en forventningskurve for strømprisen kan modelleres.  For perioden 2010 – 2013 har de daglige prisene vært slik:

 

Jeg har beregnet noen interessante nøkkeltall basert på de historiske dataene fra Nordpool spot, de står i en tabell nederst i artikkelen.  Jeg har beregnet tall på daglige priser og gjennomsnitt for uker og måneder. Naturlig nok er variabiliteten størst i de daglige observasjonene.  Enhver summering vil glatte ut ekstreme utslag.  Når jeg summerer 7 dager til et gjennomsnitt for en uke, har jeg glattet kurven.  Hvorvidt de ekstreme utslagene fra dag til dag er et problem som må tas stilling til.

Dersom du er en trader som har gjort handler som resultatføres daglig, så vil du ønske å ta høyde for de ekstreme utslagene fra dag til dag.  Og dersom du er opptatt av sluttkursene hvert kvartal, ser ut etter de faktiske kursene de dagene.  En industribedrift som ikke bryr seg om ekstreme utslag fra dag til dag, men hvorvidt den har en kraftkostnad som over tid er til å leve med, kan se på ukesprisene, månedsprisene eller kvartalprisene.

Neste spørsmål å ta stilling til er om du skal legge mer vekt på den nære historien enn på den fjerne, eller sagt på en annen måte – større vekt på 2013 enn på 2010.  Det er i dette tilfellet et viktig spørsmål – for volatiliteten i 2010 var vesentlig høyere enn i 2012.

I tillegg er det viktig å tenke over hva du tror om gjennomsnittsnivået. Det var 22 EUR høyere i 2010 enn det var i 2012.  Men her kan du få hjelp av det faktum at det finnes et likvid sikringsmarked for strømpriser.  På Nasdaq OMX commodities sine sider kan du finne den til enhver tid gjeldende prisen du kan sikre strøm på for kommende perioder.  Du kan i tillegg finne implisitt volatilitet – altså opsjonspriser der den volatiliteten markedet forventer er priset inn.  Det gjør dette til en enklere pris å modellere enn f.eks. avispapirprisen, der du verken har et likvid sikringsmarked eller implisitt volatilitet tilgjengelig.

Det er også viktig å huske at forventet variabilitet øker med tiden, og dermed bør volatilitet tidsveies.

Jeg tar følgende forutsetninger:

• Nasdaq OMX markedspris for 2014 og 2015, sluttpriser 21/10/2013.  Jeg bruker kvartalspriser, selv om jeg strengt tatt burde lagt inn en profil på prisene pr. måned.
• Utfallsrom som tar høyde for ekstremutfall.  Jeg bruker en fordeling der det settes et maksimum og et minimum, og dermed er det viktig at de ikke settes for konservativt.  For 2015 legger jeg til 5 EUR på hver side for å ta høyde for at noe som er lenger ut i tid vil at et større utfallsrom.
• En skjevhet på omtrent 0,5 i vintermånedene, siden det er sannsynlig med høyrehale (vesentlig høyere priser) og lav til litt negativ skjevhet resten av året.  Sommerprisene har til dels vært vesentlig lavere enn forventningen på Nasdaq.
• Jeg kan ikke bruke data for 2013 fullt ut, ettersom det bare er månedene januar til september det er data for.

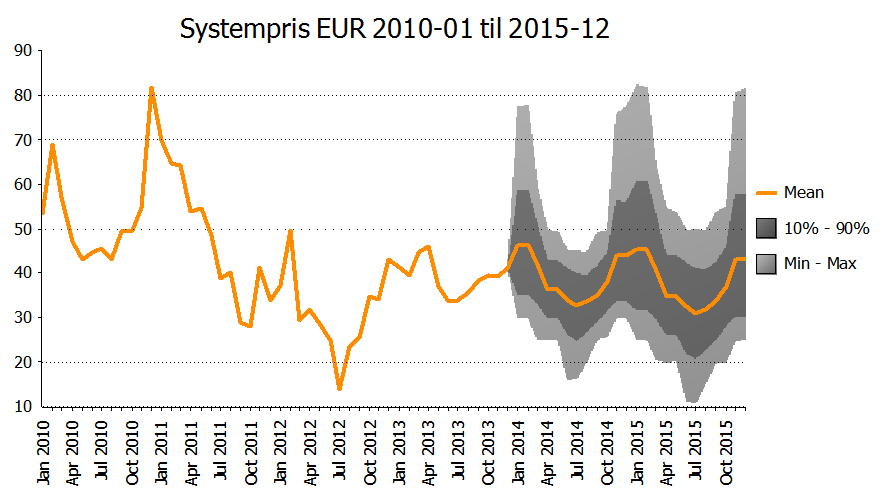
Det gir disse sannsynlighetsfordelingene:

 

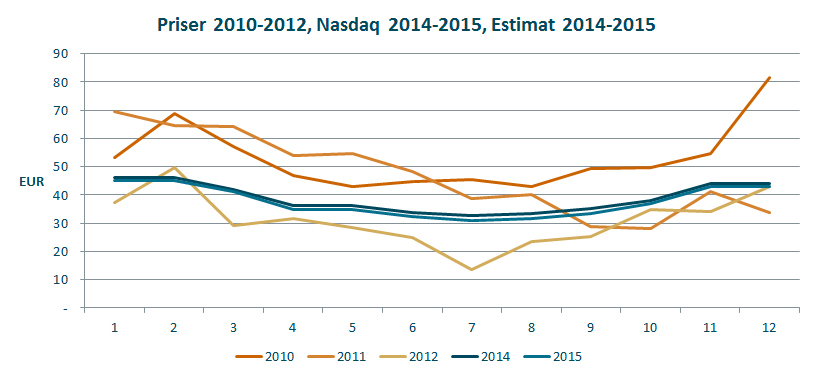
Jeg bruker faktiske priser for 2010-2012 for å rimelighetsvurdere den forventningen utfallsrommene gir:

Som grafen viser ligger estimatene lavt i forhold til 2010 og 2011, men høyere enn 2012 som var et år med historisk lave priser.  Utfallsrommet er imidlertid stort (faktisk 2010-2013 med som referanse) og det er det du bør forvente når det gjelder strømprisene.  De er svært volatile.

 

Grunnen til at jeg plotter de historiske tallene også er fordi det gir en «reality check» på den modelleringen som er gjort.  Her har jeg lagt meg tett opp til den faktiske historien, mens det andre ganger kan legges inn en forventning om en helt annen utvikling.  Uansett er det nyttig å se på hva historien har vist.

Dette er en forenklet modellering av volatiliteten i strømpriser.  Kanskje er den overforenklet, men jeg er som regel tilhenger av å forenkle snarere enn å komplisere.  Dette er dessuten en modellering av én variabel, slik at det ikke er nødvendig å modellere korrelasjoner.  Så fort du har mer enn en variabel er det en problemstilling som dukker opp, se denne artikkelen.

Jeg har tro på forenklet modellering.  Det gir bedre kontroll på hvordan usikkerhet er modellert.  Dessuten – det er uansett mange faktorer en modell ikke tar høyde for.  Det viktigste er å lage en modell som gir en god forståelse av hva det er som skaper risiko for virksomheten og der du forstår hva som foregår i modellen og de resultatene som kommer ut av den.

Data brukt i denne artikkelen:

Periode		2010	2011	2012	2013
Daglige priser	Gjennomsnitt	53,06	47,05	31,19	38,85
	Standardavvik	13,75	15,11	11,54	6,07
	Varianskoeffisient	26 %	32 %	37 %	16 %
	Skjevhet	1,81	-0,19	1,40	0,62
	Max	134,80	87,43	96,15	58,54
	Min	20,67	5,79	7,85	17,48
Gjennomsnitt uke	Gjennomsnitt	52,98	47,43	31,20	38,77
	Standardavvik	12,71	15,17	10,56	5,31
	Varianskoeffisient	24 %	32 %	34 %	14 %
	Skjevhet	1,58	-0,02	0,69	0,69
	Max	91,38	79,81	65,71	52,36
	Min	37,86	9,99	8,91	27,96
Gjennomsnitt måned	Gjennomsnitt	53,14	47,15	31,32	38,86
	Standardavvik	11,61	14,24	9,44	4,52
	Varianskoeffisient	22 %	30 %	30 %	12 %
	Skjevhet	1,65	0,21	0,20	0,42
	Max	81,65	69,62	49,59	45,91
	Min	42,89	27,95	13,70	33,46