I en modell som skal estimere risiko er det to hovedindikatorer som brukes for å beskrive den usikkerheten som ligger i variablene;

• Volatilitet; Hvor mye vil variablenes verdi kunne avvike fra forventningsverdien?
• Korrelasjon; Hvordan påvirker variablene hverandre?

Jeg har skrevet litt om volatilitet her.  I denne artikkelen vil jeg behandle modellering av den andre kjerneindikatoren på risiko – nemlig korrelasjon.

Om to variable er korrelerte betyr det at de følger et bestemt mønster når verdiene deres endrer seg.  De samvarierer på en bestemt måte.

Korrelasjon, eller samvariasjon, er i statistikk og sannsynlighetsregning et mål på styrken og retningen på den lineære avhengigheten mellom to variabler. Empirisk observert samvariasjon en nødvendig men ikke tilstrekkelig forutsetning for å avdekke om det er kausalitet (dvs. at en variabel forårsaker en annen).

Korrelasjon måles som en koeffisient fra +1 (positiv korrelasjon) til -1 (negativ korrelasjon).

Positiv korrelasjon

mellom to variable betyr at de beveger seg i samme retning

 

Negativ korrelasjon

mellom to variable betyr at de beveger seg i motsatt retning

 

En korrelasjon på 0 (nøytral)

betyr at variablene er uavhengige av hverandre

 

Korrelasjon vil bidra til økt eller redusert risiko.

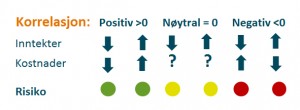Generelt vil en positiv korrelasjon mellom en inntekt og en kostnad redusere risiko.  Dersom prisen på et produkt faller, og kostnaden for å produsere det samtidig faller, så betyr det at risikoen er lavere enn ellers.  Motsatt, dersom korrelasjonen er negativ, så vil kostnaden stige dersom inntekten faller, og risikoen er dermed høyere.

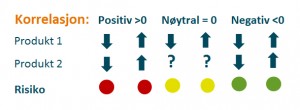Dersom to produkter har positiv korrelasjon  vil risikobildet være motsatt; om to produkter eller to kostnader samvarierer, vil det si at dersom inntekten fra det ene produktet faller, så faller også inntekten fra det andre.

Dermed er det å modellere samvariasjon særdeles viktig for å skaffe seg et godt bilde av den usikkerheten som ligger i dette selskapets kontantstrøm.

Samvariasjon kan også modelleres som regresjoner, men jeg skal se på hvordan det kan modelleres som koeffisienter til bruk i f.eks. Excel @Risk.

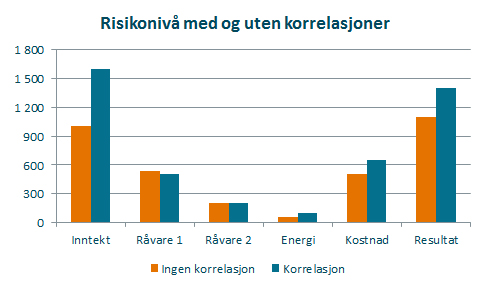
Utslagene kan bli ganske store, noe denne grafen som viser risikobildet med og uten korrelasjon:

Som grafen viser er risikoen lavere før korrelasjon introduseres i modellen.  Det kommer av at det er en positiv korrelasjon mellom de produktene selskapet selger.  Dette oppveies til en viss grad av en samvariasjon mellom kostnader og inntekter, slik at risikoen for resultatet er mindre enn summen av risikoen for inntekter og kostnader isolert sett.

Korrelasjon kan modelleres på flere måter

• Som en beregnet historisk korrelasjon
• Modelleres stilistisk for viktige variable, eller
• som nøytral (altså ingen korrelasjon)

eller som en kombinasjon av disse, avhengig av hva som beskriver samvariasjonen mellom to variable best.

Det er noen spørsmål som er viktige å stille ved bruk av historiske data for å beskrive fremtiden:

Som figuren viser er det ikke alle variable der historiske data bør brukes.  Ofte finnes det ikke gode nok data, de sammenhengene som beregnes trenger ikke være statistisk robuste, og kanskje virker de ikke logiske heller.  Dessuten er det ikke sikkert at historien beskriver fremtiden godt – det kan skje endringer som gjør at det som virket i går, ikke virker i morgen.

Det er noen fallgruver det er verdt å merke seg ved modellering av korrelasjoner:

• Korrelasjon feiltolkes som årsak, når den ikke er det.  En korrelasjon beviser ikke nødvendigvis en årsak (korrelasjon vs. kausalitet). En korrelasjon kan være en tilfeldighet som forklarer lite eller ingen ting.
  Eksempel: Om du har en høy korrelasjon mellom norske strømpriser og ølprisene i Australia, kan du dermed si at dersom norske strømpriser stiger så vil ølprisene i Australia gå opp?

• En historisk sammenheng kan bryte sammen i fremtiden, og det som forklarte fortiden vil ikke forklare fremtiden.  Verden står ikke stille.
  Eksempel: Paradigmeskifte – endringer i rammebetingelser som gjør at utviklingen vil ta en annen vei – som endring fra et regime med faste valutakurser til flytende.

• Dersom du modellerer for mange sammenhenger vil det bli vanskelig å identifisere det som virkelig driver risiko.  Fokuser på det viktigste, risikomodellering er ikke desimal-presisjon.   Det finnes ikke en modell som vil beskrive virkeligheten 100%.
  Eksempel: 20 variable skal korreleres med hverandre. Det gir en matrise på 20*20 som skal være konsistent ((Om det er en samvariasjon mellom A og B, og mellom A og C, så er det også en samvariasjon mellom B og C)). Det er nesten ikke mulig med mindre du bruker en ren dump av historiske data, eller begrenser deg og «stiliserer» sammenhengene med runde tall.

Min overordnede anbefaling for modellering av korrelasjoner er:

• Gjør en historisk analyse om du har data, men baser ikke modellen på det.  Det er alltid en fordel å vite hva historien har vist, men det trenger ikke å beskrive fremtiden godt nok.  Et unntak her er en del finansielle instrumenter der det finnes likvide markedspriser, for eksempel valutakurser.

• Modeller de viktigste variablene.  Hvilke variable driver verdiskapningen i selskapet? Det er disse du bør fokusere på å estimere sammenhengen mellom.

• Modeller korrelasjonen mellom de viktigste variablene i relativt runde tall, for eksempel
  -0,9 ((Korrelasjoner er sjelden -1 eller 1))
  -0,5
  0
  0,5
  0,9

• Gjennomgå de modellerte sammenhengene periodisk – de vil ikke forbli de samme til evig tid.  Om noe skjer, bør matrisen revideres.

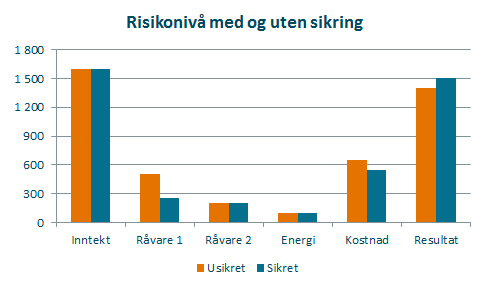
Til slutt et eksempel som belyser hvorfor det er så viktig å modellere sammenhengen mellom variable.  La oss anta at innkjøpsansvarlig i selskapet over ønsker å sikre prisen på en av råvarene selskapet bruker til å produsere produktene sine.  Det vil redusere den risikoen han har ansvaret for.  La oss anta at han sikrer 50% av kostnaden for Råvare 1.  Hva vil det si for selskapets risikobilder?

Som innkjøperen forventet så er risikoen redusert både for Råvare 1 og for kostnader i sum.  Men risikoen er ØKT totalt sett.  Det skyldes at det er en positiv korrelasjon mellom inntekter og kostnader, og dersom volatiliteten i prisen på råvarer fjernes eller reduseres, uten at det tilsvarende gjøres for inntekter, så vil resultatet være økt variabilitet totalt sett.

Det som tilsynelatende så ut som et fint, risikoreduserende tiltak er det stikk motsatte.  Det øker selskapet risiko.  Dette understreker viktigheten av å modellere sammenhengen mellom variable.  Uten det er det ikke mulig å få et godt bilde av risiko.