Da den islandske vulkanen Eyafjallajøkul i 2010 fikk et stort utbrudd, ledet det til stengte flyplasser over hele Europa, og store tap for mange flyselskaper i tillegg til betydelige problemer for flypassasjerer som ble strandet på ulike flyplasser uten å komme seg hjem.  Det nye ordet «askefast» ble en  del av norsk vokabular.

Årsakene til at fly ble satt på bakken er at mineralpartikler i asken kan forårsake skader på flymotorene som igjen kan føre til flyhavarier.  Dette skjedde i 1982, da et fly fra British Airways nesten styrtet etter å ha fått vulkanske partikler i motorene. Sannsynligvis var ikke risikoen for dette så stor, men konsekvensene ville være dramatisk dersom fly ville styrte på grunn av mineralpartikler i motorene.

Ved hjelp av simuleringssoftware og en enkel modell kan det vises hvordan risikoen forbundet med aske i luften kan beregnes, og dermed hvorfor luftrommet, selv med lav sannsynlighet for skade, ble stengt. Det er ikke beregnet følgeeffekter, siden dette ikke er en stor modell og en utfyllende analyse, men et eksempel på hvordan ulike problemstillinger kan modelleres ved hjelp av Monte Carlo simulering.   Variableverdiene er heller ikke reelle, men min egen synsing.  Målet er å vise et eksempel på modellering, ikke en presis estimering av faktisk risiko.

For å modellere risikoen ved aske i luften må det stilles noen sentrale spørsmål for å beskrive problemstillingen:

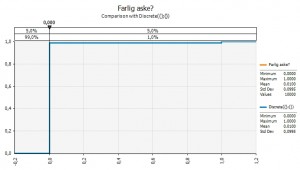Variabel 1. Er asken farlig?
Det første som må gjøres er å modellere sannsynligheten for at asken er farlig.  Det gjør jeg ved å bruke en såkalt diskret fordeling.  Den har verdien 0 dersom asken ikke er farlig, og verdien 1 dersom asken er farlig. Deretter bestemmes sannsynligheten for de to alternativene.  Jeg setter den til:

• 99% sannsynlig at asken IKKE ER farlig
• 1% sannsynlig at asken ER farlig

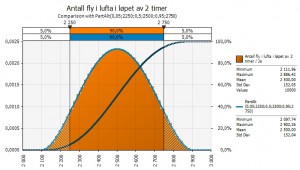Variabel 2. Hvor mange fly er i lufta?
Deretter må det sies noe om hvor mange fly som er i luften når asken treffer.  Daglig er det omtrent 30.000 fly på vingene i Europa.  Her bør vi kunne anta at dersom det begynner å styrte fly eller fly får store problemer, så vil resten umiddelbart settes på bakken. Derfor brukes bare 2/24 av disse flyene i beregningen.

Altså: 2.500 fly er i lufta når problemet oppstår.

Jeg bruker en normal fordeling, og sier at standardavviken til antall fly i lufta i en 2-timers periode er 250 fly, opp eller ned, jeg mener ingen ting om hvorvidt kurven er skjev den ene eller andre veien.

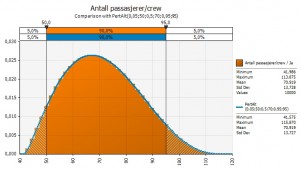Variabel 3. Hvor mange passasjerer er det i hvert fly?
Deretter må antall passasjerer og crew i hvert fly modelleres.  Jeg antar følgende:

• Gjennomsnitt antall passasjerer: 70
• Laveste antall passasjerer: 60
• Høyeste antall passasjerer: 95

Grunnen til at jeg bruker en skjev kurve her er at flybransjen har et stadig press på seg for å fylle flyene bedre. Dessuten vil selvsagt antall passasjerer variere med ukedag. Jeg mener derfor det er rimelig å anta at det er større potensial for flere passasjerer per fly enn færre.

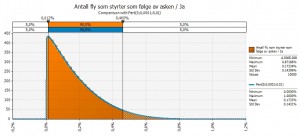Variabel 4. Hvor mange av de flyene som er i lufta styrter?
Til sist må antall fly av de som er i luften, dersom det kommer farlig aske som faktisk gjør at flyene styrter modelleres. Jeg har antatt at det godt kan være at ingen styrter, og at det er den naturlige nedre grensen.  Så har jeg antatt følgende:

• Forventet antall fly som styrter: 0,01%
• Maks antall fly som styrter: 1,0%

Da kan vi begynne å regne!

Formelen som beregner dette ser slik ut:

Hvis(«Farlig aske»=0;0)
Hvis(«Farlig aske»=1;»Antall fly i lufta» x «Antall fly som styrter» x «Antall passasjerer pr fly»)

Dersom asken ikke er farlig er Variabel 1 = 0, og ingen fly faller ned. Ingen dør altså.  Dersom asken er farlig er antall døde produktet av antall fly, antall passasjerer/crew og antall fly som styrter.

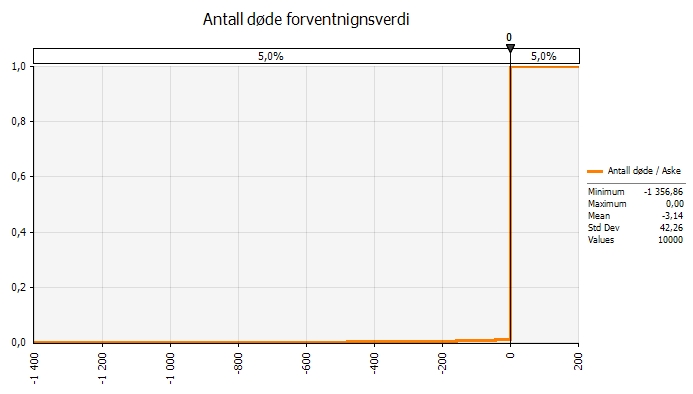
Kjørt med et simuleringsverktøy er resultatet følgende:

Som grafen viser er forventningsverdien lav, 3 passasjerer.  Det vil si at sannsynligheten for at det går riktig galt er veldig liten.  Problemet er bare at konsekvensene kan være store.  I dette scenariet, der det er 1% sannsynlighet for at asken er farlig, og 0,01% sannsynlighet for at fly styrter, er det likevel slik at det et stykke ute i halen er over 1000 passasjerer som styrter i døden.   Dette er det som kalles shortfall-risiko, og det har jeg skrevet om før. Det er noe flere eksempler på slik risiko i den posten.

Dette er en grunn til at man er forsiktig.  En annen grunn er at sannsynlighetene for både at asken er farlig og at fly vil styrte som følge av det er ukjente sannsynligheter. Dette har ikke skjedd nok ganger til at man vet.  Endring i variable har til dels store utslag.

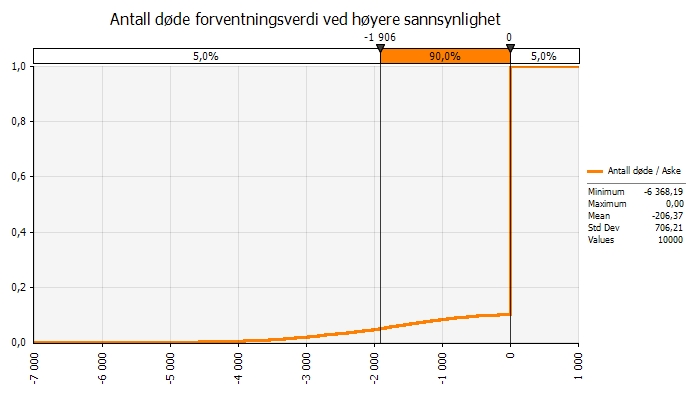
Dersom sannsynligheten for at asken er farlig er 10% i stedet for 1% og sannsynligheten for at fly faller ned er 1% snarere enn 0,1%, så vil det forventes 200 døde, eller at tre fly styrter, mens det ekstreme utslaget er 6.200 døde.

Dette er en forenklet utgave av den modelleringen som ganske sikkert ligger bak at alle flyplasser ble stengt. Hvilke sannsynligheter som legges til grunn vet jeg ikke, men a det er slik de tenker er temmelig sikkert.

Hvordan vi vurderer risikoen er avhengig av hvem vi er. Noen har stor risikoapetitt, andre har liten. Jeg er glad det ikke er meg som bestemmer om luftrommet skal stenges. Det er ikke en enkel avgjørelse.

Denne modellen er selvsagt overforenklet. Det er mange faktorer som spiller inn, som vindretning og -styrke, intensitet på utbrudd og en hel menge faktorer som som jeg ikke har oversikt over.