When the Icelandic volcano Eyafjallajøkul had a large eruption in 2010 it lead to closed airspace all over Europe, with corresponding big losses for airlines. In addition it led to significant problems for passengers who were stuck at various airports without getting home. In Norway we got a new word: “Ash stuck” ((Askefast)) became a part of Norwegian vocabulary.
When the Icelandic volcano Eyafjallajøkul had a large eruption in 2010 it lead to closed airspace all over Europe, with corresponding big losses for airlines. In addition it led to significant problems for passengers who were stuck at various airports without getting home. In Norway we got a new word: “Ash stuck” ((Askefast)) became a part of Norwegian vocabulary.
The reason the planes were put on ground is that mineral particles in the volcanic ash may lead to damage to the plane’s engines, which in turn may lead to them crashing. This happened in 1982, when a flight from British Airways almost crashed due to volcanic particles in the engines. The risk of the same happening in 2010 was probably not large, but the consequences would have been great should a plane crash.
Using simulation software and a simple model I will show how this risk can be calculated, and hence why the airspace was closed over Europe in 2010 even if the risk was not high. I have not calculated any effects following the closure, since this isn’t a big model nor an in depth analysis. It is merely meant as an example of how different issues can be modeled using Monte Carlo simulation. The variable values are not factual but my own simple estimates. The goal in this article is to show an example of modeling, not to get a precise estimate of actual risk.
To model the risk of dangerous ash in the air there are a few key questions that have to be asked and answered to describe the issue in a quantitative way.
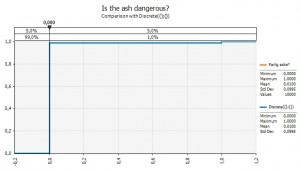 Variable 1. Is the ash dangerous?
Variable 1. Is the ash dangerous?
We first have to model the risk of the ash being dangerous to plane engines. I do that by using a so called discrete probability. It has a value 0 if the ash is not dangerous and a value 1 if it is. Then the probabilities for each of the alternatives are set. I set them to:
- 99% probability that the as IS NOT dangerous
- 1% probability that the ash IS dangerous
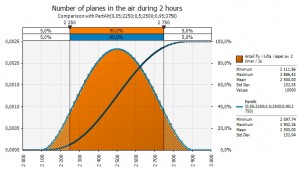 Variable 2. How many planes are in the air?
Variable 2. How many planes are in the air?
Secondly we have to estimate how many planes are in the air when the ash becomes a problem. Daily around 30 000 planes are in the air over Europe. We can assume that if planes start crashing or get in big trouble the rest will immediately be grounded. Therefore I only use 2/24 of these planes in the calculation.
- 2 500 planes are in the air when the problem occurs
I use a normal distribution and set the standard deviation for planes in the air in a 2 hour period to 250 planes. I have no views on whether the curve is skewed one way or the other. I assume it may well be, since there probably are different numbers of planes in the air depending on weekday, whether it’s a holiday season and so on, but I’ll leave that estimate to the air authority staff.
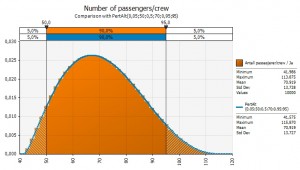 Variable 3. How many people are there in each plane?
Variable 3. How many people are there in each plane?
Thirdly I need an estimate on how many passengers and crew there are in each plane. I assume the following; I disregard the fact that there are a lot of intercontinental flights over the Eyafjallajøkul volcano, likely with more passengers than the average plane over Europe. The curve might be more skewed that what I assume:
- Average number of passengers/crew: 70
- Lowest number of passengers/crew: 60
- Highest number of passengers/crew: 95
The reason I’m using a skewed curve here is that the airline business is constantly under pressure to fill up their planes. In addition the number of passengers will vary by weekday and so on. I think it is reasonable to assume that there are likely more passengers per plane rather than fewer.
 Variable 4. How many of the planes which are in the air will crash?
Variable 4. How many of the planes which are in the air will crash?
The last variable that needs to be modeled is how many planes will crash should the ash be dangerous. I assume that maybe no planes actually crash, even though the ash gets into their engines. This is the low end of the curve. I have in addition assumed the following:
- Expected number of planes that crash: 0, 01%
- Maximum number of planes that crash: 1, 0%
Now we have what we need to start calculating!
The formula I use to calculate is as follows:
If(“Dangerous ash”=0;0)
If(“Dangerous ash”=1;”Number of planes in the air”x”Number of planes crashing”x”Number of passengers/crew per plane”)
If the ash is not dangerous, variable 1 is equal to 0, no planes crash and nobody dies. If the ash is dangerous the number of dead is a product of the number of planes, number of passengers/crew and the number of planes crashing.
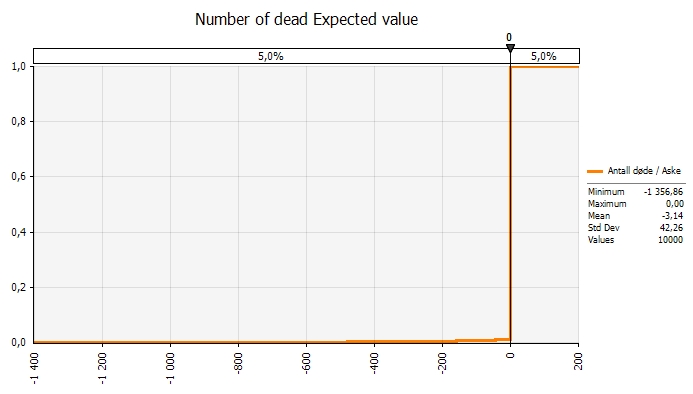
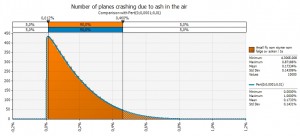
Running this model with a simulation tool gives the following result:
As the graph shows the expected value is low; 3 people, meaning that the probability for a major loss of planes is very low. But the consequences may be devastatingly high. In this model run there is a 1% probability that the ash is dangerous, and a 0, 01% probability that planes actually crash. However the distribution has a long tail, and a bit out in the tail there is a probability that 1 000 people crash into their death. This is a so called shortfall risk or the risk of a black swan if you wish. The probability is low, but the consequences are very big.
This is the reason for the cautionary steps taken by air authorities. Another reason is that the probabilities both for the ash being dangerous and that planes will crash because of it are unknown probabilities. Thirdly, changes in variable values will have a big impact.
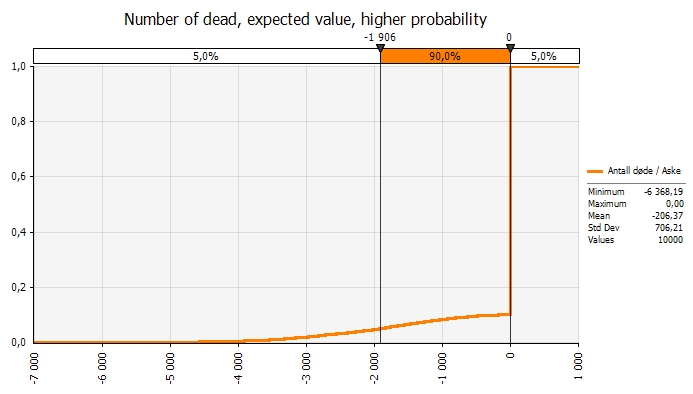
If the probability of the ash being dangerous is 10% rather than 1% and the probability of planes crashing is 1% rather than 0,01%, as much as 200 dead (or 3 planes) is expected while the extreme outcome is close to 6 400 dead.
This is a simplified example of the modeling that is likely to be behind the airspace being closed. I don’t know what probabilities are used, but I’m sure this is how they think.
How we assess risk depends on who we are. Some of us have a high risk appetite, some have low. I’m glad I’m not the one to make the decision on whether to close the airspace or not. It is not an easy decision.
My model is of course very simple. There are many factors to take into account, like wind direction and – strength, intensity of eruption and a number of other factors I don’t know about. But as an illustration both of the factors that need to be estimated in this case and as a generic modeling case this is a good example.