Hva det er? Det er tallet Phi (φ), også kalt det Perfekte tall. Dette er matematisk magi, matematisk kunst, er det mange som hevder. Og jeg er så fascinert av tall og dette tallet spesielt, at jeg tenderer til å være enig.
Altså: 1.6180339887498948482 – (1+√5)/2
Bruk dette tallet til å dele opp en linje. Altså; En linje på 10 cm, deles opp slik:
10/1,61803…….=6,18034
Fortsett på samme vis, og du før følgende interessante utvikling/tallrekke:
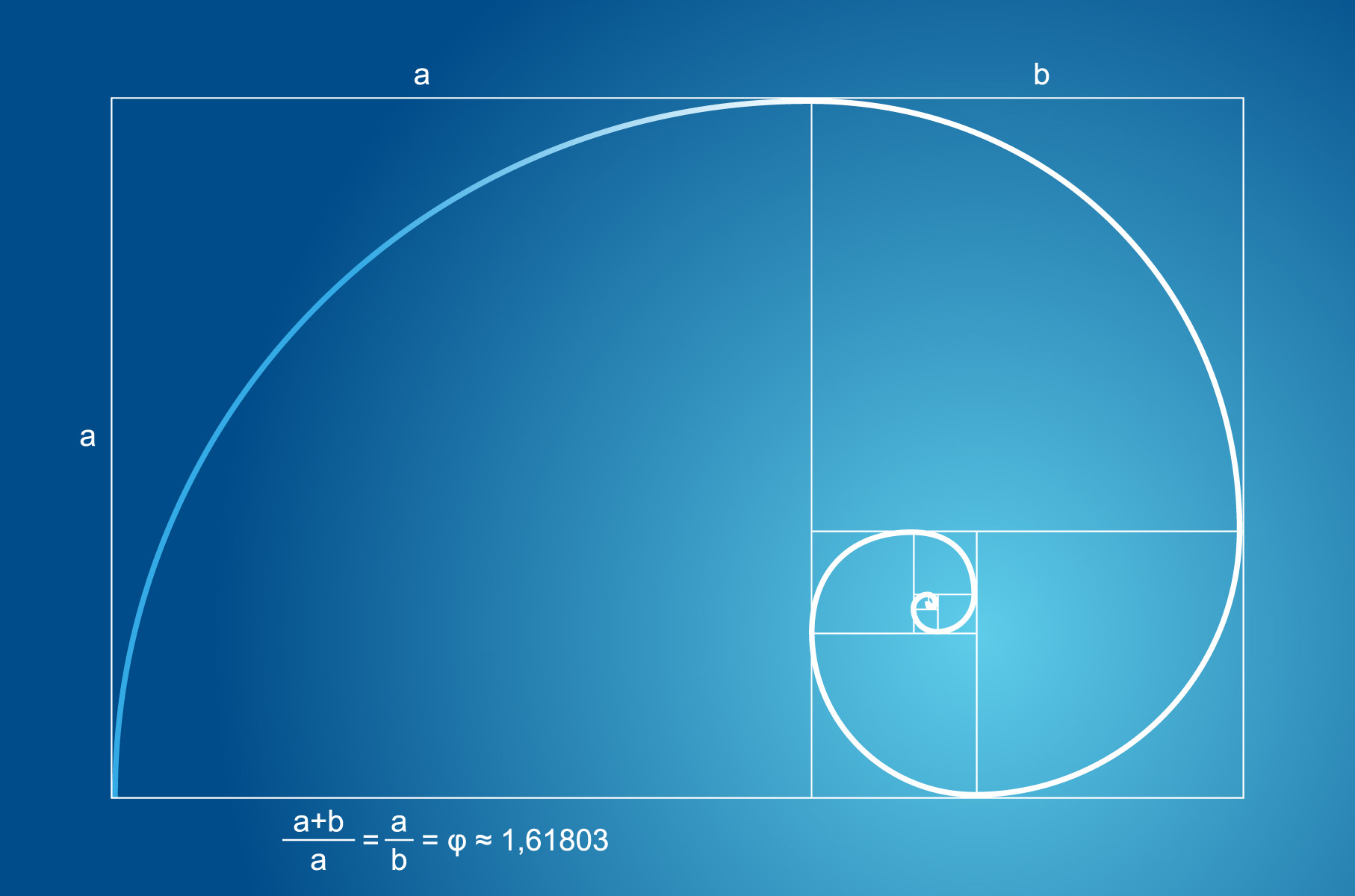
Morsomt nok er det da slik at 10-10/Phi er lik 10/Phi i neste runde, og så videre. Grafisk fremstilt ser det slik ut, følg fargene:
I tillegg må vi her introdusere Fibonacci. Dette har jeg kjent til lenge, for det brukes i analyse av aksjer og valutakurser, i såkalt teknisk analyse. Det er spesiell rekke med tall:
I en fibonacci-rekke (0, 1, 1, 2, 3, 5, 8, 13, 21, 34 …), er hvert nytt tall summen av de to foregående tallene. Ettersom du går lenger og lenger utover i tallrekken, vil forholdet mellom tallet, og tallet foran, bli tilnærmet lik Phi.
Jeg skal ikke bli for teknisk (mest fordi jeg ikke er så himla matematisk-teknisk), det matematiske er beskrevet på denne siden her. Og for all del, en myriade av andre sider. Det er knapt grenser for hvor mange treff du får om du søker på Phi eller Det gyldne snitt.
Det er mangt og meget fascinerende som kan studeres ved hjelp av Phi:

Proporsjonene i menneskekroppen
Verdens aller vakreste mennesker er studert, og man har funnet at Phi er perfekt representert i proporsjonene mellom for eksempel sentrum av pupillene og munnvikene. Dette danner et perfekt kvadrat. Tar man det gyldne snitt av dette kvadratets 4 sider, og plasserer nesetippen Phi-proporsjonalt, så finner vi et vakkert ansikt. Mest sannsynlig i hvert fall. Selv har jeg ikke tenkt å måle, ettersom det sikkert er mange feil og mangler i dette fjeset (blant annet skjev nese).
Det samme gjelder kroppen. Ta høyden, del på Phi, mål fra bakken og opp, og du bør finne navlen omtrent på det tallet. Omvendt, måler du fra hodet og ned, bør du der finne fingertuppene. Altså hos de med perfekte proporsjonerte kropper. Og det er mange andre. Og igjen, siden jeg vet at jeg ikke er perfekt, har jeg ikke tenkt å måle det, for å få akkurat det faktum bevist en gang for alle.
 Proporsjonene til mange dyrearter
Proporsjonene til mange dyrearter
Hos for eksempel delfinen faller øyet, finnen og halen innenfor gylne snitt av lengden på delfinens kropp.
Planter
Planter er bygget opp etter ficonacci-rekken, når det gjelder antall og plassering av kronblader, løv, seksjoner og frø.
DNA
DNA, koden til alt liv, er basert på Phi. Den er 34 angstrom (whatever that is, it’s small) langt og 21 angstrom bred for hver syklus i den doble spiralen. 34 og 21 er en del av fibonacci-rekken, som er tilnærmet Phi når den går mot uendelig (uendelig er forøvrig et tall tigerungen har vært fascinert av i årevis).
Solsystemet
Gjennomsnittet av gjennomsnittlig avstand (planeter går i elliptiske baner, derav gjennomsnittlig avstand) til solen for hver suksessiv planet før den er tilnærmet lik Phi.
Kunst og arkitektur
Pyramidene i Egypt har Phi-proporsjoner. Det samme har Notre Dame. Det er å finne i Leonardo Da Vincis malerier. Og apropos; Phi er å finne i Dan Browns «Da vinci koden». I bøtter og spann.
Musikk
I note-skalaer. Fioliner er laget med Phi-proporsjoner. Det musikalske klimaks i en sang er ofte å finne omtrent på phi-punktet (61,8%) i sangen, altså ikke i midten eller på slutten, som en kanskje skulle tro.
Befolkningsvekst
I byer i USA har man funnet Phi-mønstre i størrelsen på byer.
Aksjemarkedet (og andre markeder)
Phi-mønstre viser seg ofte i timingen av opp- og nedturer og prismotstandspunkter. Dette kan brukes til å tjene penger. Selv har jeg aldri fått det til, men… skal fordype meg i dette fremover.
Endringer i aksjekurser er et bilde av hva mennesker forventer om fremtiden. Studier har vist at
mennesker har positive og negative vurderinger i sine oppfatninger i Phi-forhold, med 61,8% positive og 38,2% negative.
Og det er mye mye mer.