Når du jobber med simuleringsmodeller og skal presentere disse, er ofte ikke den innebygde grafikken godt nok.  I hvert fall ønsker jeg bedre formateringsmuligheter.  Dermed dumpes simuleringsdata til et regneark, og så brukes Excels grafikkmuligheter til å lage pene presentasjonsgrafer.

Det er ikke spesielt vanskelig, men det krever litt prøving og feiling om du ikke vet hvordan.

Steg 1
Dump simuleringsdata i Excel.

Steg 2
Når du har data, må disse fordeles i siloer, eller bins.  Disse siloene skal ha lik avstand, det er slik sannsynlighetskurvens fasong fremkommer.  Fordeling i siloer kan gjøres slik:

Bestem det antall siloer du ønsker.  Jeg pleier å bruke 50, men du kan velge færre eller flere.  Finn største og minste verdi i datasettet.  Dette er yttergrensene for diagrammet ditt.  Siloene beregnes som

(Max – min)/Antall siloer

Eksempel: (1 000 – -500)/50 = 30

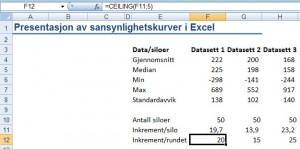
Den vil da gi deg den nøyaktige avstanden som skal være mellom hver silo, i dette eksempelet 30.  Imidlertid er sjelden tallet så rundt.  Det kan derfor være en fordel å runde opp tallet.  De kan gjøres i Excel med følgende formel ((Eksempelet har silo i F11 og minste verdi i F6)):

=CEILING(F11;5)

der det bakerste tallet sier hvordan det skal forhøyes.  I dette tilfellet forhøyes det til nærmest 5-tall.  Dette kan justeres etter hva som passer best.  Tallet i dette eksempelet var 19,7 og det ble forhøyet til 20, som er nærmeste tall delelig på 5.

På samme måte, med en litt annen formel, forhøyer eller reduserer jeg også startpunktet, det vil si den laveste verdien.

=IF(F6>0;FLOOR(F6;10);CEILING(F6;-10))

Formelen tar hensyn til muligheten for negative tall, ved at den behandler positive og negative tall ulikt.

Steg 3
Beregn sannsynlighetskurven, altså hvor mange observasjoner som faller innenfor hver silo.  Dette gjøres ved hjelp av en formel som teller hvor stor del av observasjonene som er mindre enn grensen til siloen og dele på antall observasjoner, på følgende måte:

=COUNTIF(A$17:A$10016;»<«&F18)/COUNT(A$17:A$10016)

Steg 4
Beregn frekvens, altså hvor mange observasjoner som er i hver silo. Jeg presenterer ofte både sannsynlighet og frekvens, ettersom det er mye enklere å vurdere fasongen på kurven i et frekvensdiagram.

Dette gjøres lettest ved å ta utgangspunkt i den beregnede sannsynligheten, siden frekvensen er differansene mellom akkumulert sannsynlighet på dette nivået minus akkumulert sannsynlighet på forrige nivå.

=(K18-K17)*COUNT(A$17:A$10016)

Steg 5
Lag grafikk! Som sagt er det på grunn av muligheten til pen grafikk at denne omveien brukes.

S-kurve med frekvensstolper

Merk de dataene som skal være med.  I dette tilfellet har jeg merket sannsynlighetskurven og frekvenskurven til datasett en, og setter inn et linjediagram.

1. Merk frekvenskurven, høyreklikk, bruk «Format data series», og plott serien på sekundær akse
2. Klikk på serien igjen, Design, Endre diagram-type, velg stolpediagram
3. Klikk på diagram, velg Data og legg til verdier på X-aksen
4. Høyreklikk på x-aksen, og formater verdiene slik du øsnker dem, husk at det er lurt å vise verdien 0 om det er verdier både over og under denne
5. Høyreklikk på venstre y-akse og formater. Høyeste verdi skal være 100%
6. Høyreklikk på høyre y-akse og formater. Differansen mellom tallene bør være slik at det stemmer med differansen mellom tallene på den andre Y-aksen
7. Flytt beskrivelsen fra høyre side til under diagrammet
8. Formater diagrammet ferdig

Mine ser da omtrent slik ut:

Flere S-kurver i ett diagram

For å presentere flere S-kurver i et diagram, må datasettene ha samme referanse eller X-akse, om du vil.  Dette gjøres ved at det i steg 2 iver brukes verdier for alle tre datasett for å beregne minimum og maksimum.  På disse verdiene beregnes sannsynligheten til de tre kurvene som skal plottes.  Lag gjerne et scatter-plott av disse, der du har siloverdiene på x-aksen og sannsynlighet på y-aksen.  Dette for at du skal ha kontroll på bredden i utfallsrommet – noen ganger forhøyer og reduserer Excel disse yttergrensene ganske kraftig.  Etter formatering ser diagrammet slik ut:

Vanskeligere er det ikke å lage pene sannsynlighetsdiagrammer.